Quantenchemische Verfahren zur Beschreibung der elektronischen Struktur von Materialien

Ein seit langem bestehendes Problem der elektronischen Strukturtheorie ist die Entwicklung von genauen und praktisch verwendbaren ab initio Methoden zur Beschreibung echter Materialien. Ab initio bezeichnet ein rein auf den physikalischen Gesetzen der Quantenmechanik basierendes Modell zur korrekten Beschreibung von Materialien wie beispielsweise ihrer Struktur, der chemischen Reaktivität und der magnetischen Eigenschaften. Die größte Herausforderung für genaue Vorhersagen ergibt sich durch das Phänomen der sogenannten elektronischen Korrelation im Rahmen der Quantenmechanik von Viel-Elektronen-Systemen. Wird die elektronische Korrelation nicht korrekt beschrieben, so kann das zu qualitativ falschen ab initio Vorhersagen von physikalischen und chemischen Eigenschaften führen.

Was ist elektronische Korrelation und warum ist ihre Beschreibung so kompliziert? Elektronische Korrelation ergibt sich aus der Tatsache, dass sich Elektronen voneinander abstoßen. Somit entstehen Teilchenverteilungen, deren Komponenten permanent untereinander wechselwirken. Das bedeutet beispielsweise Folgendes: Befindet sich ein Elektron zu einem Zeitpunkt an der Position r, ist es weniger wahrscheinlich ein weiteres Elektron zum selben Zeitpunkt in unmittelbarer Nähe zu finden. Für Zwei-Elektronen-Systeme lässt sich elektronische Korrelation noch relativ einfach beschreiben. Für den Fall eines Moleküls oder Festkörpers muss die elektronische Korrelation jedoch für sehr viele Elektronen richtig beschrieben werden. Es handelt sich dabei um ein Problem von exponentieller Komplexität. Die quantenmechanische Beschreibung von einfachen Molekülen wie zum Beispiel Methan (CH₄), welches lediglich zehn Elektronen besitzt, ist bereits eine große rechenintensive Herausforderung. Größere Moleküle und Festkörper sind noch um vieles aufwendiger. Das Fe-Porphyrin Molekül in Abbildung 1 würde beispielsweise 37 000 TB RAM zur Speicherung einer hinreichend genauen elektronischen Wellenfunktion benötigen. Dieser Speicherbedarf steht selbst in den modernsten Supercomputerzentren der Welt nicht zur Verfügung.

Diese exponentielle Barriere zu überwinden, stellt eine der größten Herausforderungen für die computerorienterte Physik und Chemie dar. Die Abteilung "Theorie der elektronischen Struktur" am Max-Planck-Institut für Festkörperforschung entwickelt und erweitert Theorien, um dieses Problem zu lösen. Hier entwickeln die Forscher Methoden, die auf Konzepten von Quanten-Monte-Carlo-Verfahren und Quantenchemie [1] basieren und die die Energetik von komplexen Molekülen, Festkörpern und Oberflächen mit großer Effizienz äußerst genau beschreiben.

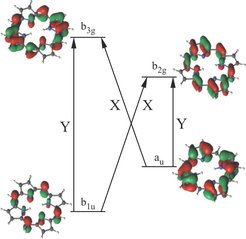
Im vergangenen Jahr konnten wir nennenswerte Fortschritte in dieser Richtung erzielen. Von zwei ausgewählten Arbeiten werden wir hier kurz berichten. Um die hochkomplexe elektronische Wellenfunktion im Rahmen der Configuration-Interaction-Methode zu beschreiben und ebenso die Orbitalformen zu optimieren, wurde ein Quanten-Monte-Carlo(QMC)-Verfahren entwickelt. Anhand der optimierten Orbitale lassen sich chemische Bindungen interpretieren. Dieses QMC-Verfahren ist eine Erweiterung der Full-Configuration Interaction QMC Methode, die Alavi und seine Kollegen seit 2009 [2, 3] entwickeln. Die Orbitaloptimierung basiert auf der quantenchemischen CASSCF-Methode (complete-active-space self-consistent-field). Die daraus resultierende Hybridtechnik [4–6] wird als CIQMC-CASSCF-Methode bezeichnet und wurde verwendet, um selbst große Moleküle wie Fe-Porphyrin (siehe Abb. 1) zu untersuchen. Natürliche Porphyrine sind ein Schlüsselmaterial für die Photosynthese (Chlorophyll), die Atmung (Hämoglobin) und den Elektronentransport (Cytochrome). Daher spielen diese Moleküle eine zentrale Rolle im Leben. Synthetische Porphyrine werden ebenso aufgrund ihres Potenzials zur Anwendung in Solarzellen, als Katalysatoren zur Wasserspaltung und sogar als molekulare Schalter untersucht. Wegen ihrer fundamentalen Bedeutung wurden bereits umfangreiche experimentelle und theoretische Untersuchungen der elektronischen Spektren von Porphyrinen durchgeführt.

Eine der wichtigsten Konsequenzen der elektronischen Korrelation ist die Verschränkung von elektronischen Konfigurationen mit geringen Energiedifferenzen und großer räumlicher Distanz. Das führt zu dramatischen Änderungen der Frontorbitale des Moleküls, welche hauptsächlich die Reaktivität und Bandlücke bestimmen und somit, bei welcher Frequenz Licht absorbiert wird. Die Chemie der angeregten Zustände ist ebenfalls sehr stark durch elektronische Korrelation beeinflusst. Mit unserer FCIQMC-CASSCF Methode lassen sich die Frontorbitale und das Anregungsspektrum des Porphyrin Moleküls sehr genau bestimmen (siehe Abb. 2).

Mittels FCIQMC-CASSCF lassen sich verschränkte Systeme beschreiben, die sich mit konventionellen Quantenmethoden nicht mehr erfassen lassen. Zusätzlich zu Porphyrin-Molekülen untersuchen wir auch Cuprate, die Phänomene wie Antiferromagnetismus und Supraleitung bei relativ hohen Temperaturen aufweisen.

Elektronische Korrelation kann auch zu langreichweitigen Wechelwirkungen führen, die in Festkörpern einen nicht vernachlässigbaren Beitrag zur Grundzustandsenergie liefern. Solche van-der-Waals-Wechselwirkungen akkumulieren sich und sind daher trotz der relativ schwachen Beiträge für viele Materialien wie etwa Graphit von wesentlicher Bedeutung, um deren Stabilität zu erklären. Um diese Effekte korrekt zu beschreiben, müsste man aber viele Hunderte bis Tausende Elektronen explizit korrelieren. Das ist selbst mit einfacheren quantenchemischen Methoden wie der Coupled-Cluster-Theorie nicht möglich. Wir haben dennoch ein Verfahren entwickelt, anhand dessen sich aus der elektronischen Wellenfunktion eine einfachere Funktion zur korrekten Beschreibung solcher langreichweitigen Korrelationseffekte ableiten lässt [7].

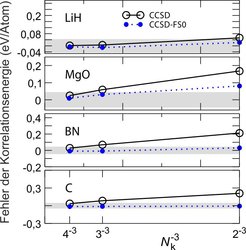
Mithilfe von Interpolationsmethoden können wir abschätzen, wie sich elektronische Wechselwirkungen im Festkörper als Funktion von sehr großen interelektronischen Abständen verhalten, und mithilfe eines Modells eine Korrektur zur Grundzustandsenergie berechnen. Abbildung 3 zeigt, dass diese Korrektur es ermöglicht, konvergierte Coupled-Cluster (CCSD)-Korrelationsenergien zu erhalten, selbst wenn man nur die Elektronen von relativ kleinen Kristallzellen explizit beschreibt. Mit diesen Entwicklungen wird es möglich sein, Phasendiagramme für Materialien unter hohen Drücken vorherzusagen.

Literaturhinweise