Numerische Simulationen zum Verstehen und Vorhersagen der Eigenschaften von Nanostrukturen

Einleitung

Eine Nanostruktur wird üblicherweise als ein Objekt definiert, das entlang einer Dimension kleiner als etwa 100 Nanometer ist. Mit dieser Definition befinden sich nanostrukturierte Systeme überall um uns herum und sind bereits in der Technologie weit verbreitet. Viele Chemiker arbeiten mit Molekülen, deren Ausmaße dieser Definition entsprechen. Unter den Begriffen Nanophysik oder Nanochemie verbirgt sich jedoch mehr also nur eine Charakterisierung bezüglich der Objektgröße. Unter „Nano“ versteht man die Skala, bei der die Materialeigenschaften erheblich von den Volumeneigenschaften des Festkörpers abweichen. Dabei verschwinden die Grenzen zwischen Materialwissenschaften, Physik und Chemie und Annäherungen an historisch getrennte Gebiete wie die Molekularbiologie (manchmal als Nanowissenschaft der lebendigen Organismen bezeichnet) finden statt. Die neuen Phänomene, die aufgrund der Reduzierung der Atomanzahl beobachtet werden, lassen sich in zwei Kategorien einteilen. Zum einen sind es Veränderungen der bekannten Eigenschaften, wie z. B. der plastischen Verformbarkeit des Werkstoffes. Dabei können auch drastische Veränderungen vorkommen, die man als qualitative Veränderung bezeichnen kann, wie beispielsweise die Veränderung der Kristallstruktur bei Reduzierung der Dimension. Zum anderen sind es fundamental neue Eigenschaften, die aufgrund quantenmechanischer Effekte auftreten. Diese Effekte (wie z. B. das Tunneln von Ladungsträgern) werden in der Regel bei sehr kleinen Längenskalen relevant und können die Eigenschaften dominieren.

Das Verständnis der physikalischen und chemischen Prozesse auf der Nanometer-Skala ist heutzutage einer der aktivsten Bereiche der Forschung. Die Gründe liegen dabei auf der Hand: Der Zugang zu dieser neuen Skala ist von fundamental wissenschaftlicher Bedeutung, um ein grundlegendes Verständnis dieser neuen Phänomene zu erlangen. Andererseits ist die technologische Bedeutung der gewonnenen Erkenntnisse enorm und oft mit direkten Auswirkungen auf die industrienahe Forschung verbunden.

Vom Standpunkt eines Theoretikers aus gesehen, ist das Gebiet der Nanophysik und Nanochemie attraktiv, da man dort an der Grenze unseres Verständnisses forscht. Jedoch ist diese Längenskala – zwischen der Welt der Moleküle und der des Festkörpers – nur schwer zugänglich. Für beide gibt es akkurate Lösungsansätze, aber die intermediäre Skala ist herausfordernd. Die Strukturen sind in einer Dimension oft nicht größer als wenige Atomlagen und machen eine atomistische Behandlung wünschenswert, beinhalten aber in ihrer Gesamtheit meist tausende bis hunderttausende Atome. Weiterhin stellen viele experimentell relevante Größen, wie optische Eigenschaften und Transport, sogenannte Anregungen dar. Diese Anregungen sind für eine große Anzahl an Atomen äußerst schwierig zu berechnen.

Numerische Methoden

Die atomistische Berechnung der quantenmechanischen elektronischen Eigenschaften hat mit der Entwicklung der Dichtefunktionaltheorie (DFT) [1, 2] eine Formulierung angenommen, die mit einem verhältnismäßig geringen numerischen Aufwand auskommt. Diese Methode wird oft als ab initio bezeichnet, was bedeutet, dass lediglich die Kernladungszahl und die Masse der Atome als Eingabe notwendig sind. Die für diese Methode übliche Näherung für die Elektronen-Korrelation – die Näherung der lokalen Dichte (LDA) – ist in vielen Fällen zufriedenstellend.

Basierend auf DFT-Rechnungen ist es möglich Pseudopotenziale zu entwickeln (Abb. 1a), die Ergebnisse mit einer Genauigkeit von DFT liefern (Abb. 1b), die aber numerisch weniger aufwendig sind. Wenn dabei auf eine selbstkonsistente Lösung und auf die Berechnung der Gesamtenergie verzichtet wird, können Zustände nahe der Bandlücke für Strukturen mit 10⁶ Atomen berechnet werden [3]. Diese Zustände nahe der Bandkante sind für optische Eigenschaften und Transportphänomene verantwortlich. Aus den DFT-Zuständen kann jedoch nur der Grundzustand angemessen beschrieben werden. Im Experiment wird das System aber stets angeregt, um es zu untersuchen. Optische Experimente wie die Absorption oder Emission von Licht sind z. B. sehr verbreitet. Um diese Experimente zu verstehen, muss die theoretische Behandlung weitere Vielteilcheneffekte berücksichtigen. Diese werden meistens in zwei Kategorien unterteilt.

Das Quasiteilchen-Bild und die Bandstruktur

Zum einen spricht man von Quasiteilchen-Effekten. Um dieses Konzept zu verstehen, soll zunächst angemerkt werden, dass die experimentelle Bandstruktur eines Festkörpers mit einer Änderung der Elektronenzahl verknüpft ist. Bei der Photoemission wird z. B. Licht auf den Festkörper eingestrahlt und die Energie und der Impuls der austretenden Elektronen untersucht. Die gemessene Bandstruktur charakterisiert also Übergänge von Systemen mit N Elektronen zu Systemen mit N-1 Elektronen (oder umgekehrt). Die Energie eines Quasiteilchens entspricht genau der Energiedifferenz der beiden Systeme. Dieses Quasiteilchen-Konzept ist nützlich, da es einen direkten Zusammenhang zur experimentell gemessenen Bandstruktur liefert. Dieser Zusammenhang ist jedoch nicht bei Methoden gegeben, die nur auf der Grundzustandsdichte eines durch die Elektronenzahl N definierten Problems basieren, wie in der DFT. In der Vielteilchentheorie beschreiben die Pole der Green'schen Funktion gerade diese Übergänge. Diese können durch eine Vielteilchen-Störungstheorie in der sogenannten GW-Näherung [4] berücksichtigt werden. Als Grundlage für das ungestörte System dienen dabei oft die Ergebnisse der DFT. Der Unterschied zwischen dem ungestörten und dem exakten System wird durch eine Reihenentwicklung eines geeigneten Operators dargestellt. Im Festkörper wird in der Störungsreihe nicht das nackte Coulomb-Potenzial, sondern eine durch den Festkörper abgeschirmte Coulomb-Wechselwirkung W angenommen. Bei geringer Störung, bei der der DFT-Ausgangszustand eine gute Näherung für den exakten Zustand darstellt, liefert die GW-Näherung bereits in erster Ordnung gute Ergebnisse. Zum Beispiel wird die direkte und inverse Photoemission von vielen Halbleitern in der GW-Näherung gut reproduziert.

Angeregte Zustände, Exzitonen

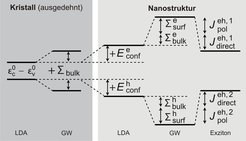
Zum anderen gibt es Effekte, die mit der Wechselwirkung zwischen diesen Quasiteilchen zu tun haben. Wenn ein Elektron durch eine optische Anregung (absorbieren eines Photons) vom Valenzband in das Leitungsband übergeht, wechselwirkt es mit dem verbleibenden Loch im Valenzband. Dieses Loch (also ein fehlendes Elektron) ist positiv geladen, während das Elektron negativ geladen ist und die Wechselwirkung ist attraktiv. In ausgedehnten Halbleitern ist dieser Effekt meist relativ klein (die Wechselwirkung liegt energetisch im meV-Bereich) und das Quasiteilchen-Bild der Bandstruktur bleibt relativ genau.

Bei Nanostrukturen oder Molekülen kann aber die Wechselwirkungsenergie sehr groß werden (im eV-Bereich), da Elektron und Loch auf einem engen Raumbereich lokalisiert sind und dementsprechend stark überlappen. Eine schematische Darstellung der verschiedenen Energiebeiträge zur Exzitonenergie ist in Abbildung 2 wiedergegeben. Die theoretischen Lösungsansätze dieser Probleme sind die Bethe-Salpeter-Methode und quantenchemische Verfahren, wie die Interaktion der Konfigurationen.

Anwendungsbeispiel: Erzeugung verschränkter Photonen

Nachdem ein Überblick über die Methoden und Verfahren gegeben wurde, soll nun die Anwendbarkeit der Methode an einem Beispiel demonstriert werden. Dazu dient das Gebiet der selbstorganisierten Quantenpunkte (QP) aus Halbleitermaterial. Durch den Unterschied in den Gitterkonstanten zweier Halbleiter kann eine verspannte nanoskalige Struktur eines Halbleiters in einen anderen Halbleiter eingebettet werden. In unserem Fall handelt es sich um einen InAs-QP in einer GaAs-Matrix. Die Ladungsträger – sowohl die Elektronen als auch die Löcher – lokalisieren im InAs-QP. Um die Struktur zu beschreiben, werden über zwei Millionen Atome benötigt, da sowohl die Atome innerhalb des Quantenpunktes (typischerweise 50.000 Atome) als auch ein hinreichend großer Bereich außerhalb dieser Struktur berücksichtigt werden müssen.

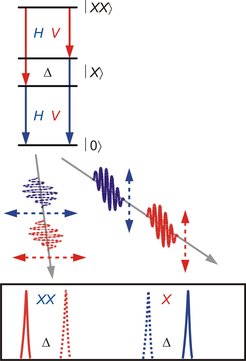
Eine der möglichen Anwendungen solcher QP liegt im Bereich der Quanteninformation sowie der Erzeugung und Manipulation von verschränkten Quantenzuständen. Ein weitverbreiteter Vorschlag [5] ist die Verwendung von Halbleiter-Quantenpunkten als Quelle für verschränkte Photonen. In Abbildung 3 ist die Grundidee schematisch dargestellt. Polarisationsverschränkte Photonen werden dabei durch die Emissionskaskade Biexziton, Exziton, Grundzustand (│XX>→│X>→│0>) generiert. Die Polarisation (V oder H) des Photonenpaares wird durch den Spin des Exzitonenzustandes bestimmt. In einem idealisierten QP mit entarteten Exzitonenzuständen ist die Polarisation des ersten Photons (aus dem │XX>→│X> Zerfall) verschränkt mit der Polarisation des zweiten Photons (aus dem │X>→│0> Zerfall). Dieser Vorschlag beruht daher auf der Existenz einer verschwindenden exzitonischen Feinstruktur. Dies ist jedoch a priori nicht gegeben. In der Tat unterliegen Elektron und Loch einer Austauschwechselwirkung, die in der Regel zu Aufspaltungen der Exzitonen-Zustände führt. Es wird intensiv danach geforscht, die Feinstrukturaufspaltung (FSA) [6] des Exzitons zu reduzieren.

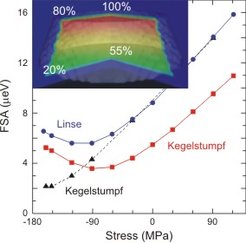
Mithilfe von Pseudopotenzialen und Berechnungen im Rahmen der Interaktion der Konfigurationen konnte gezeigt werden [7], dass in einem Quanten-Draht, der entlang der [111]-Richtung gewachsen wurde, oder in einem QP, der auf einem (111)-Substrat aufgewachsen wurde (beide mit C_3v-Symmetrie), die FSA aufgrund der Struktur-Symmetrie verschwinden muss. Unser Vorschlag – Strukturen mit C_3v-Symmetrie [7] zu verwenden – resultiert (für die meisten experimentellen Gruppen) in der Verwendung neuer Arten von Strukturen. Obwohl diese Strukturen bereits existieren, besteht ein Anreiz, die gut untersuchten [001]-Strukturen beizubehalten und stattdessen die FSA mithilfe externer Felder zu minimieren. Ein möglicher Ansatz ist dabei, die Probe auf kontrollierte Weise zu verspannen, indem sie auf einem piezoelektrischen Kristall aufgewachsen wird. Dabei können die exzitonischen Zustände gegeneinander energetisch verschoben werden. Wir konnten zeigen [8], dass im Fall von Quantenpunkten, die aus einer Halbleiterlegierung mit der niedrigen C₁-Symmetrie bestehen, die beiden Zustände sich einer vermiedenen Kreuzung unterziehen (Abb. 4). Die zentrale Frage ist dabei, wie klein die FSA durch Verspannungsfelder werden kann. Um eine quantitative Antwort auf diese Frage zu erhalten, wurde die FSA für verschiedene Drücke und verschiedene QP berechnet (Abb. 4). Es konnte gezeigt werden, dass für realistische Strukturen die FSA auf ein Minimum von etwa 2 µeV reduziert werden kann – eine Vorhersage, die später experimentell bestätigt werden konnte [9].

An diesem Beispiel wurde illustriert, dass moderne numerische Verfahren in der Lage sind, für einige experimentell relevante Größen, Vorhersagen zu treffen und so unser Verständnis der zugrundeliegenden Physik zu erweitern.