Die Ausnützung von Größeneffekten für die elektrochemische Energieumwandlung

Einleitung

Elektrochemische Energieumwandlung beruht darauf, dass ein chemischer Vorgang, der Energie liefert, elektrochemisch geführt wird. Beispiele sind die Knallgasreaktion H₂+O₂→H₂O oder die Reaktionen in der Lithiumbatterie, in der Lithium von einer Phase (z. B. metallisches Lithium) in die Partnerphase (FePO₄) überführt wird. Dies soll im Folgenden näher beleuchtet werden: Der direkte Kontakt zweier reaktiver Phasen führt zu einer irreversiblen Reaktion, die die Reaktionsenergie in Form von Wärme freigibt. Die Ausnützung dieser Wärme z. B. in Form von elektrischer Energie ist nicht nur umständlich, sondern auch durch einen schlechten Wirkungsgrad charakterisiert. (Maximal ist dieser Wirkungsgrad durch den Carnot-Wirkungsgrad gegeben.) Im Prinzip der gleiche Vorgang wird – mit gleichen Nachteilen – in Gang gebracht, wenn die beiden Reaktionsphasen durch ein Medium getrennt sind, das im ersten Beispiel Wasserstoff (H) oder Sauerstoff (O) oder im zweiten Beispiel Lithium (Li) durchlässt; dies kann durch Membranen geschehen, die sowohl ionisch (H⁺, O^2-, Li⁺) wie auch elektronisch leitfähig sind. Der Trick der elektrochemischen Zelle beruht nun darauf, dass diese Membran eine Elektrolytmembran ist, die also lediglich das Ion, aber nicht das Elektron durchlässt. Somit wird das Elektron auf den Weg durch den äußeren Draht gezwungen, auf welchem es direkt elektrische Arbeit leisten kann. Hierbei wird die gesamte Triebkraft der Reaktion in elektrische Arbeit umgesetzt. Das Verhältnis von Output (elektrische Arbeit bzw. Triebkraft) zu Input (chemische Energie) ist in vielen Fällen theoretisch nahe 100%. (Im Prinzip kann dieser Wert wegen der Reaktionsentropie sogar überstiegen werden.)

Bei all diesen Devices benötigt man Materialien, die nur, aber sehr gut, Ionen leiten sowie Materialien, die sowohl Ionen als auch Elektronen leiten. In der elektronischen Prozesskette ist der Transport lediglich ein einziger, wenn auch kinetisch häufig ganz wesentlicher Schritt; hinzu kommen u. a. Grenzflächenreaktionen wie Sauerstoffreduktion, Wasserstoffoxidation oder die Umladung von Lithium.

All diese Elementarprozesse lassen sich, wie in unserem Arbeitskreis ausgiebig gezeigt, durch Widerstände und Kondensatoren parametrisieren, wobei es sich im Allgemeinen nicht um rein elektrische Elemente handelt, sondern etwa um elektrochemische Widerstände oder chemische Kapazitäten.

Diese Parameter sind nun sowohl explizit wie auch implizit von der Größe der Partikel abhängig. Zum einen sind sie proportional einer Potenz der Transportlänge: Bekannterweise ist der elektrische Widerstand im simpelsten Fall dieser Länge (L) proportional, die elektrische Kapazität diesem invers proportional mit dem Resultat, dass das Produkt, die sogenannte elektrische Relaxationszeit, unabhängig davon ist. Im Fall des chemischen Transportes – z. B. von Li (= Li⁺+e^–) – in einem Festkörper sind beide proportional L und damit die Diffusionsrelaxationszeit proportional zu L². Zum zweiten sind diese Parameter auch proportional zu einer effektiven Materialkonstante (z. B. die effektive spezifische Leitfähigkeit eines komplexen Phasengemenges), die aufgrund subtilerer Effekte drastisch von L abhängen können.

I. Optimierte Speichermorphologie für Lithiumbatterien

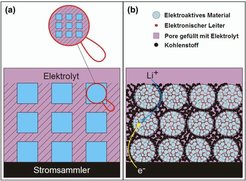
Lassen Sie uns zuerst die explizite Abhängigkeit untersuchen und drei experimentelle Beispiele angeben, die diese verifizieren. Trivialerweise wird der Elektrolytwiderstand verringert, wenn man die Dicke verkleinert, allerdings stößt man hier schnell an praktische Grenzen, vor allem bedingt durch mechanische Stabilität. Dennoch sind Dünnschicht-Brennstoffzellen oder -Batterien wichtige Anwendungen. Viel deutlicher ist der optimierte Größeneffekt in Bezug auf die Speichergeschwindigkeit von Li-Elektroden. Es sei daran erinnert, dass die Speicherzeit proportional zum Quadrat der Dicke ist. Partikel, bei denen die Li-Speicherung aufgrund der bei Raumtemperaturen in der Regel schlechten Transport-Materialkonstanten Jahre oder Jahrzehnte dauerten, lassen sich durch Verkleinern auf Nanogröße im Subsekundenbereich füllen. Allerdings ist es nötig, sowohl Li⁺ als auch e^- an all diese Abermillionen von Teilchen schnell heranzubringen. Der schnelle Antransport von Li⁺ ist in aller Regel durch einen Flüssigelektrolyten gewährleistet. Der Elektronentransport kann jedoch ein ernstes Problem darstellen, wenn die elektronische Leitfähigkeit der Partikel nicht sehr hoch ist (wie z. B. für TiO₂ oder LiFePO₄).

Hier ist es nötig, „effektiv gemischt-leitende Netzwerke“ zu erzeugen, für die wir Lösungen verschiedener Dimensionalität realisiert haben.

Beispiel I–1: Abbildung 1 zeigt hierarchisch-poröses TiO₂ (Anode), das mit metallisch leitfähigem RuO₂ auf der Nanoskala verdrahtet ist [1]. Entsprechendes gelingt auch mit dem Kathodenmaterial LiFePO₄.

Beispiel I–2: Ähnlich effizient sind Kohlenstoffnanokabel, die mit TiO₂ beschichtet sind. Das elektrochemische Speicherverhalten ist hier wie bei der eben beschriebenen Morphologie auch bei sehr hohen Strömen ungewöhnlich gut [2].

Beispiel I–3: Das dritte Beispiel betrifft Zinn [3, 4]. Zinn kann im Prinzip sehr viel Li aufnehmen. Allerdings ist es in makroskopischer Form wegen der beachtlichen Volumenexpansion nicht zu verwenden, die zum Aufbrechen der Partikel und zum Kontaktverlust führt. Die in Abbildung 2 gezeigte Morphologie – Sn-Nanopartikel in Kohlenstofffasern – schlägt gleich sechs verschiedene Fliegen mit einem Schlag.

(i) Die Partikel sind klein genug, um eine schnelle Li-Diffusion zu gewährleisten. (ii) Die Kohlenstofffasern stellen elektronische Leitungspfade zur Verfügung. (iii) Die Ionen können schnell auf die Oberfläche derselben gelangen, haben – um zu den Sn-Partikeln zu gelangen – nur eine sehr kurze Distanz zurückzulegen und können durch den Kohlenstoff hindurchtreten. (iv) Die Partikel sind, obwohl elektrochemisch verbunden, mechanisch entkoppelt. Damit entfällt die Problematik der Volumenänderung. (v) Die Kohlenstofffaser hält die Partikel zusammen (Binder-Effekt). (vi) Da die Zinn-Ionen (Sn⁴⁺) wohl nicht im Kohlenstoff beweglich sind, entfällt auch die Problematik des elektrochemischen Ostwald-Reifens, ein in der Regel übersehener Mechanismus, der normalerweise zur kinetischen Instabilität kleiner Elementkristallite in der Elektrolytlösung führt.

Von fundamentalem Interesse für die Festkörperforschung sind naturgemäß die impliziten Größeneffekte, die in unserem Kontext in der Regel entweder durch das von uns etablierte generalisierte Raumladungsmodell erklärbar und behandelbar sind oder auf Kapillareffekte zurückgehen. Auch hierzu drei Beispiele.

II. Größeneffekte auf Materialkonstanten und ihre Relevanz für Lithiumbatterien

II.1: Neue Elektrolyte mit hoher Leitfähigkeit und hoher Überführungszahl

Elektrolyte für Hochleistungs-Lithiumbatterien sind wegen der Nanostrukturierung der Elektroden (wie oben ausgeführt) bevorzugt flüssig. Hier ist unser „Soggy-Sand-Elektrolyte“-Konzept [4] vielversprechend (Abb. 3).

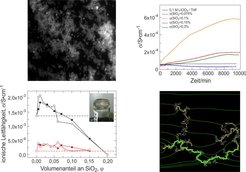
Diese Elektrolyte stellen Dispersionen von SiO₂-Partikeln in lithiumsalzhaltigen organischen Lösemitteln dar. Die Zumischung der SiO₂-Partikel zu üblichen Flüssigelektrolyten hat eine Reihe von Vorzügen. Zunächst kann spektakulärerweise die Ionenleitfähigkeit ansteigen. Dieser Effekt beruht auf der Adsorption von Anionen auf den SiO₂-Oberflächen, wodurch Ionenpaare zerstört und die Lithiumionen daraus befreit werden. Der Effekt ist natürlich auch mechanisch sehr vorteilhaft, weil eine günstige semi-feste Konsistenz erreicht wird, die zudem der Benetzung kaum abträglich ist. Zudem steigt der relative Anteil der Kationenleitfähigkeit an der Gesamtleitfähigkeit, d. h. der Anteil der Kationen selbst in Bereichen, wo die Leitfähigkeitserhöhung durch eine zu hohe Partikeldichte zunichte gemacht wird. Die Verringerung der Anionenleitfähigkeit ist nämlich per se sehr wichtig, da eine solche zu einem Konzentrationsgefälle im Elektrolyten führt, was letztendlich sogar ein Auskristallisieren des gelösten Salzes zur Folge haben kann. Eine wesentliche Voraussetzung für diese Effekte ist die Ausbildung und Stabilität des Oxid-Netzwerkes. Unsere experimentellen Arbeiten über Polyethylenglykol als Lösemittel geben zusammen mit Monte-Carlo- und Finite-Elemente-Rechnungen Aufschluss über die wesentlichen diesbezüglichen Vorgänge. Für weitere Details sei auf die Literatur [5, 6] verwiesen. Hier sei nur erwähnt, dass wir kürzlich die Ausbildung oxidischer Netzwerke zum ersten Mal über Ionenleitfähigkeitsmessungen verfolgen konnten. Dieser Anstieg der Leitfähigkeit durch Wachsen des Netzwerkes wird üblicherweise von einer teilweisen Verringerung auf einer größeren Zeitskala gefolgt, welche auf einer Vergröberung des Netzwerkes beruht. In geeigneten Fällen jedoch kommt diese Vergröberung sehr schnell zum Stillstand [6].

II.2: Speicherung in Nanokompositen

Die gleichen Raumladungseffekte, die in eben diskutiertem Beispiel in Leitfähigkeitseffekten resultierten, führen auch zu der Möglichkeit, Lithium in Grenzflächennähe zu speichern, auch wenn keine der Phasen (Phase 1 und Phase 2) dies einzeln vermag. Dies beruht auf dem von uns vorgeschlagenen „Job-Sharing“ der beiden Phasen: Die Randschicht der Phase 1 speichert e^–, die der zweiten Phase das Li⁺. Es ist evident, dass damit ein bedeutender Materialfreiheitsgrad für die Speicherung erschlossen wurde [7, 8]. Inwieweit dieser Mechanismus für Anwendungen relevant sein wird, wird die Zukunft zeigen. Auf alle Fälle lässt sich mit einem solchen Mechanismus ein geeigneter Kompromiss zwischen Speicherkapazität und (Ent-)Ladegeschwindigkeit schließen, die sich in Batterien und Suprakondensatoren komplementär verhalten.

II.3: Zellspannungseffekte in grenzflächendominierten Systemen

Während die Zellspannung von solchen Raumladungszonen unberührt bleibt, wird sie wesentlich vom Kapillardruck abhängen, den kleine Teilchen aufweisen. Dieser innere Druck führt zu einer Variation der Zellspannung, die der inversen Partikelgröße proportional ist. Hochinteressant in dem Zusammenhang sind amorphe Materialien. Die Zellspannungsvariation kann hier sehr groß sein und lässt sich durch den Verlust der langreichweitigen Wechselwirkung erklären, interessanterweise aber auch durch Kapillareffekte, wenn nominelle Partikelgrößen atomistischer Größenordnung in Rechnung gestellt werden (Abb. 4) [9].

Solche Überlegungen werfen einen neuen Blick auf den Übergang von Nanosystemen verschiedener Phasen zu einphasigen Systemen, in denen sich obige Phasen als Komponenten wiederfinden.

III. Größeneffekte bei Brennstoffzellen

Am Ende seien Größeneffekte bei Brennstoffzellen adressiert, wobei wir nochmals auf geometrische Effekte zurückkommen. Die in Abbildung 1 aufgeführten Parameter sind natürlich auch von der Fläche abhängig. Ein simples, aber wirksames Phänomen, ist die Erhöhung der Reaktionsrate durch erhöhte Oberfläche der Elektrokatalysatoren sowohl im Anoden- wie im Kathodenraum. Speziell für die Sauerstoffreduktion in Hochtemperaturbrennstoffzellen haben wir durch die Kombination von Experimenten mit reaktionskinetischen und atomistischen Modellierungen detaillierte Vorstellungen zur Reaktionskinetik gewonnen. So ist beispielsweise bei oxidischen Kathoden die Präsenz und Beweglichkeit von Sauerstofffehlstellen von enormer Wichtigkeit für die Kinetik der Sauerstoffreduktion. Somit ist nicht nur die Kontaktfläche sondern auch das Ladungsträgerverhalten am Kontakt für die Reaktionskinetik entscheidend. Letztere kann selber durch den Parameter Größe variiert werden, entsprechend einem impliziten Effekt auf die Reaktionskonstanten. Systematische Untersuchungen bestätigen dies und erlauben sogar die Voraussage und Verifizierung besserer Elektrokatalysatoren [10]. Am Beispiel der Hochtemperaturbrennstoffzellen haben wir zeigen können, dass die Variation der Größe in solchen Fällen so prägnant sein kann, dass dies nicht nur zur Variation der lokalen Parameter führt, sondern sogar zum Wechsel im dominanten Mechanismus.