Verspannte Nanostrukturen aus Halbleitern

Zwei- und dreidimensionale Quantenpunktkristalle

Beim epitaktischen Wachstum von Indium-Gallium-Arsenid (InGaAs) auf Gallium-Arsenid (GaAs)-Substraten bilden sich auf der Oberfläche aufgrund der hohen Verspannung spontan nanometerkleine InGaAs-Inseln - so genannte Quantenpunkte. Diese selbstorganisierten Quantenpunkte sind defektfrei und könnten daher in zukünftigen Halbleiterbauelementen eine wichtige Rolle spielen. Die Bildung der Quantenpunkte geschieht jedoch zufällig auf der Oberfläche, was es erheblich erschwert, die Quantenpunkte einzeln und gezielt zu funktionalisieren. Es ist uns nun gelungen, diese Quantenpunkte durch Wachstum auf vorstrukturierten Substraten streng periodisch in allen drei Raumrichtungen anzuordnen [1].

Abbildung 1 zeigt im unteren Teil die Rasterkraftmikrospie-Aufnahme einer strukturierten GaAs (001)-Oberfläche. Die Strukturierung besteht aus einem regelmäßigen Lochmuster, mit einer Periodizität von 200 nm und einem Lochdurchmesser von 50 nm.

Werden Quantenpunkte auf eine solche Oberfläche gewachsen, bilden sie sich exakt an den Positionen, die durch die Löcher vorgegeben wurden. Nach dem Wachstum von drei Schichten InAs-Quantenpunkten, die jeweils durch eine 15 nm dicke GaAs-Zwischenschicht getrennt sind, erhält man die Oberfläche, die im oberen Teil der Abbildung 1 gezeigt ist. Es ist gut zu erkennen, dass die Quantenpunkte das Muster der Löcher übernommen haben. Die laterale Anordnung der Quantenpunkte pflanzt sich in Wachstumsrichtung durch den Kristall fort. Diese Replikation in vertikaler Richtung führt zu einem dreidimensionalen "Quantenpunktkristall", in dem die Quantenpunkte in allen drei Dimensionen periodisch angeordnet sind [1].

Laterale Verspannungsfeldinterferenzen

Bei der lateralen Anordnung der Quantenpunkte werden diese in eine feste räumliche Beziehung zueinander gestellt. Dabei beobachteten wir, dass die starken Verspannungsfelder, die die Quantenpunkte umgeben, miteinander interferieren. Diese Interferenz ist abhängig vom lateralen Abstand der Quantenpunkte. Abbildung 2 vergleicht Theorie und Experiment für zwei unterschiedlich große Einheitszellen von periodischen Quantenpunktfeldern. Die Simulation berechnet die Verspannungsfeldlandschaft auf der Oberfläche, nachdem die Quantenpunkte mit GaAs bedeckt wurden. Das Experiment dagegen zeigt eine Rasterkraftmikroskopie-Aufnahme der Oberfläche, nachdem eine zweite Quantenpunktschicht auf die bedeckte erste Quantenpunktschicht abgeschieden wurde. Die hellen Bereiche in der Simulation sind synonym für Verspannungsfeldminima und die hellen Flächen im Experiment geben die Positionen der InGaAs-Quantenpunkte an. Es ist klar ersichtlich, dass sich für die große Periode neben den Hauptminima auch kleinere elongierte Satellitenminima ausbilden. Da Quantenpunkte bevorzugt an Orten entstehen, die eine möglichst geringe Verspannungsenergie aufweisen, konnte in diesem Experiment die laterale Wechselwirkung von Verspannungsfeldern eindeutig nachgewiesen werden [2]. Das erlangte Verständnis dieser Wechselwirkung ist eine wichtige Voraussetzung für eine zukünftige Hochintegration einzelner Quantenpunktbauelemente auf einem einzelnen Chip.

Silizium-Germanium: Erweiterung des Wellenlängenbereichs und leistungsfähige Tunneldioden

Selbstorganisierte Germanium (Ge)-Inseln, eingebettet in einem Silizium (Si)-Kristall, könnten Grundsteine für eine moderne Si-basierte Mikroelektronik werden. Im Folgenden untersuchen wir die optischen Eigenschaften solcher Ge-Inseln. Wir benutzen dafür die Photolumineszenz-Spektroskopie, bei der die Probe mit Laserlicht angeregt, und das abgestrahlte Licht spektral zerlegt und detektiert wird. Solche Spektren wurden bei tiefen Temperaturen (1,4 K) aufgenommen und sind in Abbildung 3 (Hintergrund) für Si-Überwachstumstemperaturen von 250°C bis 500°C dargestellt. Dabei stammt das dominante Signal von den eingebetteten Inseln. Im Vordergrund ist die Energie des dominanten Signals als Funktion der Si-Überwachstumstemperatur gezeigt. Man erkennt eine systematische Verschiebung der Spektren zu niedrigeren Energien (längeren Wellenlängen), wenn die Ge-Inseln bei geringeren Temperaturen überwachsen werden. Bei einer Temperatur von 250°C senden die Ge-Inseln zum Beispiel Licht bei Wellenlängen größer als 2 μm aus [3, 4], was einer Energie entspricht, die um mehr als 100 meV kleiner ist als die Bandlücke (E_g) von Ge. Dies ermöglicht die Herstellung von elektrisch betriebenen lichtemittierenden Dioden (LEDs), die in einem deutlich erweiterten Wellenlängenbereich emittieren als dies bis jetzt auf Si-Basis möglich war [5].

SiGe-Heterostrukturen können außerdem dazu dienen, die Leistungsfähigkeit von Esaki-Dioden deutlich zu verbessern [6]. Der Bandkantenverlauf einer Esaki-Diode ist in Abbildung 4(a) dargestellt. Durch die extrem hohe p- und n-Dotierung entsteht eine ausgeprägte Bandkantenverbiegung, die dazu führt, dass beim Anlegen einer Spannung ein Tunnelstrom von Elektronen im entarteten Leitungsband in das entartete Valenzband fließen kann. Wird die angelegte Spannung weiter erhöht, so wird der Tunnelstrom unterdrückt und nur ein geringer Reststrom kann fließen. Ein Maß für die Güte einer Esaki-Diode ist daher das Verhältnis zwischen Tunnel- und Reststrom. Die Tunnelstromstärke hängt entscheidend von der Tunnelbarriere (schwarzes Dreieck) ab. Besteht die undotierte Zone aus SiGe, so wird die Tunnelbarriere aufgrund der kleineren Bandlücke von SiGe deutlich abgesenkt, und ein größerer Tunnelstrom kann fließen.

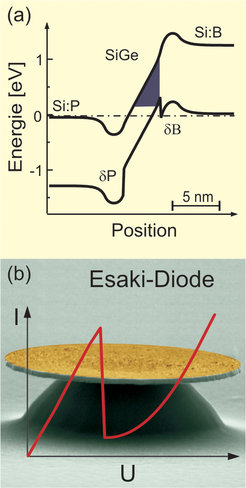
Eine auf semi-isolierendem Si-Substrat prozessierte Esaki-Diode ist in Abbildung 4(b) dargestellt. Die oberste Metallschicht, die aus Titan und Gold besteht, bildet den Kontakt für die elektrische Charakterisierung. Die beste bei Raumtemperatur gemessene Strom-Spannung-Kennlinie ist in Abbildung 4(b) dargestellt und besitzt ein Tunnel- zu Reststrom-Verhältnis von 6:1 (bei 4 K sogar mehr als 7:1). Ohne SiGe erzielt man Verhältnisse von maximal 2:1. Ein Bereich negativ differentiellen Widerstandes, in dem der Strom abnimmt, wenn die Spannung erhöht wird, ist deutlich zu erkennen. Bauelemente mit negativ differentiellen Widerständen, wie zum Beispiel die Esaki-Diode, können Anwendung in der Hochfrequenzelektronik oder in digitalen Schaltkreisen finden.

Aufgerollte Halbleiternanoröhren als radiale Übergitter und Nanopipelines

Die Herstellung von nanometergroßen Objekten durch das Ablösen dünner Schichten von ihrem Substrat hat in den letzten Jahren einige Aufmerksamkeit erregt [7, 8]. Dabei werden zum Beispiel verspannte Halbleiterbischichten epitaktisch auf eine Opferschicht auf einer Substratoberfläche mittels Molekularstrahlepitaxie (MBE) aufgewachsen. In einem zweiten Schritt werden durch lithographische Verfahren Muster auf der Oberfläche definiert, und die Probe anschließend in ein Ätzbad gelegt. Die Ätze ist so gewählt, dass sie selektiv die Opferschicht entfernt und somit die Halbleiterbischicht vom Substrat ablöst. Die intrinsische Verspannung der Schichten führt dazu, dass sie sich während des Ablösens verbiegen und sich, wie in der japanischen Papierfaltkunst Origami [9], selbständig zu dreidimensionalen Objekten auffalten. Die Position und Form der Struktur wird von dem vorher aufgebrachten Muster bestimmt. Eine interessante Struktur, die hier näher untersucht werden soll, sind Nanoröhren, die aus mehrfach aufgerollten dünnen Bischichten entstehen (im Englischen: rolled-up nanotubes RUNT).

Um eine Vorstellung über mögliche Anwendungen dieser neuartigen Nanoröhren zu bekommen, ist eine strukturelle Untersuchung ihres Aufbaus notwendig. Hierbei interessieren wir uns insbesondere für den mikroskopischen Aufbau der Nanoröhrenwand [10]. Eine mächtige Methode zur strukturellen Untersuchung ist die Transmissionselektronenmikroskopie (TEM), bei der analog zum Lichtmikroskop, die Probe mit Elektronen durchstrahlt wird, und die entstehende Abbildung aufgenommen werden kann. Dank des verwendeten Elektronenstrahls kann eine nahezu atomare Auflösung erreicht werden. In Abbildung 5 ist eine Collage verschiedener TEM-Aufnahmen zweier RUNTs zu sehen.

Abbildung 5(a) zeigt eine Übersichtsaufnahme einer untersuchten Nanoröhre. Diese hat drei Umdrehungen während des Aufrollens durchgeführt, und ihr Innendurchmesser beträgt 200 nm. Abbildung 5(b) zeigt die Struktur der Wand mit höherer Vergrößerung. Die mit "I" gekennzeichneten Bereiche weisen das regelmäßige Muster des GaAs-Kristalls auf (Vergrößerung siehe Abb. 5(c)). Daneben gibt es die Bereiche "II", in denen das Bild keine regelmäßigen Muster zeigt. Offensichtlich sind in diesen Bereichen die Atome nicht periodisch angeordnet, ähnlich wie in einem Glas. Diese ungeordneten Bereiche entstehen, wenn sich beim Aufrollen die extrem dünne Halbleiterbischicht auf sich selbst legt, d.h. wenn sich die Nanoröhre beim Aufwickeln mehr als einmal um die eigene Achse gedreht hat. Bei diesem Vorgang legt sich die Schicht nicht einfach auf die vorherige Wicklung, sondern die Atome der einzelnen Schichten bilden eine Bindung aus. Da die periodische Anordnung der Atome aber von Schicht zu Schicht leicht gegeneinander versetzt ist, verliert die neu gebildete Grenzschicht diese Periodizität.

Die Abfolge von wohl geordneten, kristallinen Bereichen und nicht geordneten, glasartigen Bereichen mit jeweils Dicken von wenigen Nanometern stellt eine neuartige Materialstruktur dar. Wie viele Perioden in einer solchen "Überstruktur" möglich sind, zeigt Abbildung 5(d). Hier folgen 10 geordnete und ungeordnete Bereiche aufeinander, sodass eine Wandstärke von etwa 45 nm entsteht. Der Einschub in Abbildung 5(d) zeigt die Nanoröhre, in der die gezeigte Wandstruktur gefunden wurde.

Neben der strukturellen Charakterisierung ist das Ausloten von möglichen Anwendungsgebieten der RUNTs von großem Interesse. Eine Anwendungsmöglichkeit wäre der Transport von Flüssigkeiten auf Oberflächen [11]. Abbildung 6(a) zeigt eine Lichtmikroskopie-Aufnahme zweier aufgerollter Nanoröhren. Die beiden RUNTs liegen parallel zu einem Graben, der die Startkante für den Aufrollprozess vorgegeben hat. An der Stelle "A" hat die Grabenkante einen Knick, sodass die Halbleiterbischicht in zwei verschiedenen Richtungen aufrollt. Die gewählte Grabengeometrie kann daher Nanoröhren wohl definierter Länge an wohl definierten Positionen erzeugen. Die RUNTs haben einen Innendurchmesser von 100 nm. Da sie sich über eine Distanz von etwa 11 μm aufgerollt haben, besitzen sie über 30 Wicklungen. Mit einer feinen Glaspipette (1 μm Durchmesser) wurde ein Tropfen Farbstoff auf die Oberfläche aufgebracht. Dabei wurde der Tropfen so platziert, dass er nur die Öffnungen der RUNTs bedeckt, die sich gegenüberliegen (Abb. 6(b)). Ein Fluoreszenzbild des Farbstoffs ist in Abbildung 6(c) zu sehen. Beide Nanoröhren sind deutlich zu erkennen, obwohl der Farbstoff nur auf die Öffnungen platziert wurde. Dies Ergebnis bedeutet, dass der Farbstoff durch Kapillarkräfte in die Nanoröhren gesaugt wurde. Hierbei fällt auf, dass von der oberen Nanoröhre nur die ersten 25 μm gefüllt sind, während die untere über die gesamte Länge von 50 μm aufgefüllt wurde. Der Grund ist in der Vergrößerung in Abbildung 6(b) zu sehen. Die obere Nanoröhre besitzt genau an der Stelle, bis zu der der Farbstoff eingezogen wurde, einen etwa 180 nm großen Defekt, der ein weiteres Auffüllen verhindert.

Literatur

[1] Kiravittaya, S., H. Heidemeyer und O. G. Schmidt: Physica E 23, 253 (2004).

[2] Heidemeyer, H., U. Denker, C. Müller und O. G. Schmidt: Physical Review Letters 91, 196101 (2003).

[3] Denker, U., M. Stoffel, O. G. Schmidt und H. Sigg: Applied Physics Letters 82, 454 (2003).

[4] Stoffel, M., U. Denker, G. S. Kar, H. Sigg und O. G. Schmidt: Applied Physics Letters 83, 2910 (2003).

[5] Stoffel, M., U. Denker und O. G. Schmidt: Applied Physics Letters 82, 3236 (2003).

[6] Duschl, R. und K. Eberl: Thin Solid Films 380, 151 (2000).

[7] Schmidt, O.G. und K. Eberl: Nature 410, 168 (2001).

[8] Prinz, V. Y., V. A. Seleznev, A. K. Gutakovsky, A. V. Chehovskiy, V. V. Preobrazhenskii, M. A. Putyato und T. A. Gavrilova: Physica E 6, 828 (2000).

[9] Schmidt, O. G., N. Schmarje, C. Deneke, C. Müller und N. Y. Jin-Phillipp: Advanced Materials 13, 756 (2001).

[10] Deneke, Ch., N. Y. Jin-Phillipp, I. Loa und O. G. Schmidt: Applied Physics Letters 84, 4475 (2004).

[11] Deneke, Ch. und O. G. Schmidt: Applied Physics Letters, im Druck.