To exist or not to exist

How can we tell if materials are thermodynamically stable?

September 27, 2024

Stability is crucial in many aspects of life, from determining if political systems will undergo revolutions to assessing whether ecosystems might collapse or if houses can withstand earthquakes. In physics, determining whether a material is thermodynamically stable—resistant to changes in its state—is a complex task. For quantum materials this stability can depend on various factors such as temperature, physical and chemical composition, and external pressure, among others. Traditionally, stability criteria are determined using mathematical derivatives, involving extensive calculations to understand how different properties change under various conditions—a truly formidable task.

In our research, we have shown that calculating a single quantity can effectively assess a material’s stability. This quantity, called the two-particle generalized susceptibility, provides all the necessary information about the material’s stability from just one set of conditions. This novel, compact approach offers an alternative way to answer the classic Shakespearean question for materials: to exist or not to exist?

Thermodynamic stability is a crucial concept for condensed matter systems. The conventional formulation of stability criteria relies on derivatives of thermodynamic potentials, i.e., on the Hessian matrix of the grand potential Ω.

In the textbook example of the liquid-gas transition, the stability of the van der Waals isotherms in the pressure-vs-volume plane can be directly inspected by calculating the isothermal compressibility, which can be expressed with the second derivative of the grand potential w.r.t. the volume. Similar considerations extend also to many-electron systems in the presence of a local Coulomb interaction. The latter induces metal-to-Mott insulator transitions at finite doping, close to which two derivatives are needed in order to set the stability conditions at a fixed temperature.

Figure 1. Sketch of the phase diagram of the two-orbital Hubbard model as a function of temperatureT, interaction U, and chemical potential μ. The U-axis is located at half-filling and T = 0. At finite doping, the violet “moustache”-shaped region describes a coexistence regime of a weakly correlated and a strongly correlated (Hund’s) metal. — Figure 1. Sketch of the phase diagram of the two-orbital Hubbard model as a function of temperature T, interaction U, and chemical potential μ. The U-axis is located at half-filling and T = 0. At finite doping, the violet “moustache”-shaped region describes a coexistence regime of a weakly correlated and a strongly correlated (Hund’s) metal.

Figure 1. Sketch of the phase diagram of the two-orbital Hubbard model as a function of temperature
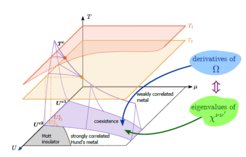
T, interaction U, and chemical potential μ. The U-axis is located at half-filling and T = 0. At finite doping, the violet “moustache”-shaped region describes a coexistence regime of a weakly correlated and a strongly correlated (Hund’s) metal.

In this Letter, we show that it is indeed possible by calculating eigenvalues of local two-particle vertex functions. Even though a direct connection with the thermodynamic potentials is not obvious at first sight, here we demonstrate that the conditions based on the Hessian can be rewritten solely in terms of the single-particle propagator G and the eigenspectrum of the generalized twoparticle susceptibility χ (see right-hand side of the sketch in Figure 1).

This new method of assessing stability simplifies an otherwise complex task and provides a fresh perspective on understanding the behavior of quantum materials. By reducing the problem to calculating a single, key quantity—the two-particle generalized susceptibility—we bypass the need for laborious computations involving multiple derivatives. This approach not only offers a more practical tool for researchers but also deepens our understanding of how different phases of matter emerge and interact. As we continue to explore these intricate materials, this compact criterion could serve as a reliable guide for predicting stability and phase transitions, bringing us closer to unraveling the mysteries of condensed matter physics.