"Everything should be made as simple as possible, but not simpler." – A computational perspective on the fruit fly of electronic correlations

In a recent review, an international team of scientist gives a perspective on the progress of numerical analysis on the Hubbard model, a minimal model for electronic correlations, over the last two decades.

Reductionism not only is a well-known theoretical scientific paradigm. It also gives, like Einstein’s famous quote, practical guidance for tackling complex problems: reduce the problem at hand to its fundamental constituents before trying to solve it. In reality this often goes hand in hand with finding so-called model systems that capture the essence of the complex phenomenon to be analyzed. A prominent example is the Drosophila melanogaster (commonly known as fruit fly), which has only four pairs of chromosomes, making it particularly suited for studying classical genetics.

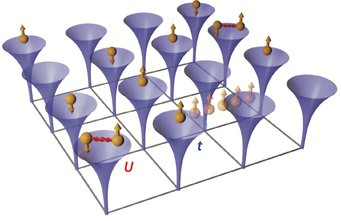
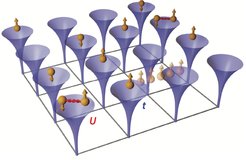
Biological systems are not the only example for complexity in nature. In solid-state physics so-called strongly correlated systems display a wealth of fascinating phenomena: quantum magnetism, high-temperature superconductivity, quantum criticality and transitions from metals to insulators. Many of these phenomena arise due to the intriguing interplay between the motion of electrons in a crystal and the mutual repulsion that those electrons feel due to their negative charge. The Hubbard model is to strongly correlated systems what the fruit fly is to classical genetics: a minimal theoretical model system that captures the essential physics. In the Hubbard model the solid is seen as a periodic lattice on which electrons can tunnel (“hop”) from one lattice site to another with an amplitude t. The Coulomb interaction between the electrons is treated quite crudely: whenever two electrons sit on same lattice site, an energy penalty of a certain amount U has to be paid.

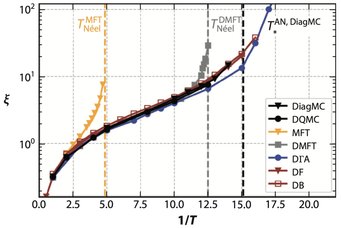
Despite its simplicity, the Hubbard model displays a lot of the intriguing phenomena occurring in strongly correlated systems listed above. In particular, it displays strong antiferromagnetic spin fluctuations which characterize the phase diagram of cuprates and are believed to mediate high-temperature superconductivity. However, the Hubbard model is only solvable exactly in limited regimes, like one spatial dimension. In a more material realistic settings often approximative methods have to be used to reveal its properties. Due to huge advancements in both computational power and algorithmic development over the last three decades, numerical approaches often become the methods of choice. These advancements are summarized in a recent review compiled by a team of international scientist and published in Annual Review of Condensed Matter Physics.

“Apart from methods like Monte Carlo simulations of finite size lattices and perturbation theory, other powerful approximations exist,” says Thomas Schäfer, leader of the independent Max Planck research group “Theory of Strongly Correlated Quantum Matter" and coauthor of the review. “A particularly prominent one is the dynamical mean-field theory. This method has been the first one that could consistently describe the metal-insulator transition induced by the electron-electron repulsion in the Hubbard model, the so-called Mott transition”. The essence of the dynamical mean-field theory is to take a single atom embedded in a non-interacting medium as a representative for the entire lattice. The method becomes exact in the limit of infinite dimensions (infinitely many neighbors of the atom) and this description works particularly well when the strength of the Coulomb interaction is large.

“Another powerful numerical method is the functional renormalization group”, says Sabine Andergassen, professor for quantum many-body theory at the University of Tübingen, coauthor of the review. “It describes the evolution from a solvable initial problem to the problem of interest and can efficiently tackle nonlocal correlations relevant in low dimensions and especially in quantum critical regimes.” Due to the approximations introduced in practical implementations, the validity of the functional renormalization group is, however, usually limited to the weak-coupling regime.

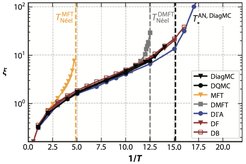
These two contrasting advantages of the dynamical mean-field theory and functional renormalization group can be seen as a prototype for the recent search for consensus of a large variety of different methods (“multi-method studies”). “Different methods can be used in tandem in order to be able to provide an efficient and unbiased treatment of many-body correlations of arbitrary intensity and spatial extensions,” Schäfer says. “This has shifted the perspective of the field towards more collaborative projects of the respective experts in different methods.”

Apart from giving a (necessarily non-exhaustive) summary of the past advancements, the review also poses relevant challenges to be addressed by future research on the Hubbard model like the interplay of correlations and different lattice types, the competition between different types of instabilities, the calculation of response functions on the real frequency axis (which is necessary to compare directly to experiments) and more realistic models for quantum materials.

“Although there has been a lot of progress over the past decades, the physics of the Hubbard model still fascinates researchers and is far from being completely understood”, Schäfer says. “The new generation of scientists will hopefully profit from this review as a starting point for working on this challenging problem.”